Research
- Climate Variability
- Weather types
- North Atlantic Oscilation
- Blocking events
- Storm-tracks
- Cut-off low systems
- Climate extremes
- Vegetation dynamics
- Atmopsheric Rivers
- Nonlinear Analysis
- Natural Hazards
- Datasets
Nonlinear Analysis
The analysis of observed and simulated climatic field time-series have exhibited features and patterns that are typical from non-linear complex multidimensional stochastic systems (Franzke and OíKane, 2017). The physical understanding and statistical modeling of regularities extracted from atmospheric-oceanic data is quite relevant, in particular: 1) the simplification of the information description, its compression onto low-dimensional spaces and the modelling of extremes; 2) the assessment of predictable long-range features, the teleconnections and their impacts, both in the present and during possible future climatic scenarios, 3) the improvement of multivariate non-Gaussian probability distributionís fitting to geophysical data and its application in statistical downscaling and data assimilation
Since 2007, the climatology and climate change group of IDL has developed novel statistical techniques with relevance into the above three referred topics, leading to several publications on high level journals and formation of PhD and MSc degree students.
We present bellow a set of highlighted research results.
The multivariate statistical dependence among surface-Earth variables and large-scale oceanicatmospheric indices has been assessed with computation, both of nonlinear, asymmetric correlations and Information-Theory measures (e.g. mutual information) from reanalysis datasets. An example is given by Pires and Perdig„o (2007) who have computed joint pdfs of the monthly precipitation and of the North Atlantic Oscillation (NAO) index thus putting into evidence their nonlinear and non-Gaussian interdependence (Fig. 1).

Fig. 1. Contours of a Maximum-Entropy joint estimated pdf between the monthly DJF precipitation and NAO index. The asymmetric NAO forcing is evident (Pires and Perdig„o 2007).
The relatively reduced length of available climatic datasets may lead to an overestimation of the statistical links among variables due to the presence of joint outliers or other artifacts. Therefore, and by looking for the suppression of that effect, we have built maximum entropybased estimators of the nonlinear correlations and mutual information. The effects of noise, sampling and finite data size have been assessed in Pires and Perdig„o (2012, 2013)
Nonlinear complex systems allow a vast plethora of non-evident inter-relationships, lying much beyond the common bivariate linear response upon a systemís forcing. This was witnessed through non-Gaussian statistical signatures (e.g. triadic and polyadic correlations) of emergent behaviors, coming from synergies, not explained by pairwise links. An example of that was shown, coming from triadic wave resonances in a simple chaotic dynamical atmospheric model (Pires and Perdig„o, 2015). Fig. 2 shows, pdf iso-surfaces of a triad of variables under the presence of a synergy. The multivariate synergies launch the possibility of new kinds of predictability features in the climatic system.
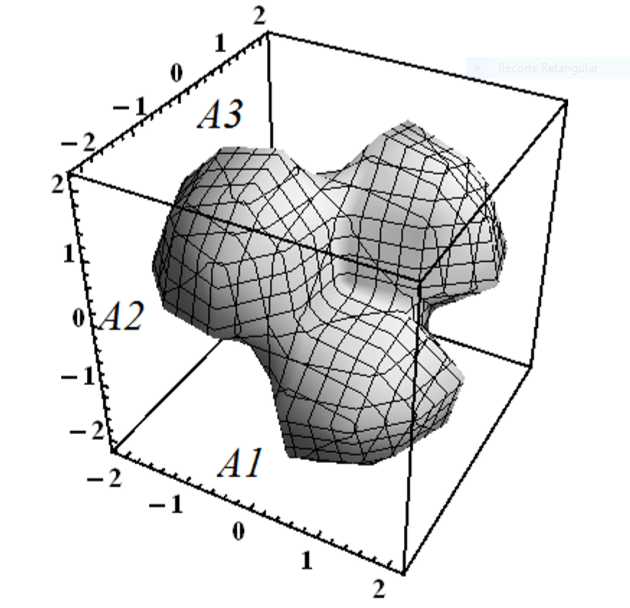
Fig. 2 Iso-surfaces of the pdf of a perfect triad (A1, A2, A3) with pair-wise independent variables (Pires and Perdig„o, 2015).
Nonlinear and non-Gaussian systems call for advanced techniques of efficient source separation or multivariate dataset decomposition, that are far beyond the traditional Empirical Orthogonal Function (EOF) Analysis. That is relevant to disentangle independent mixed signals (stochastic sources), coming from independent forcings, and which are merged an observed time-series. For that, tools based on Information-Theory tools and Projection-Porsuit techniques, such as the Independent Component Analysis (ICA) and Independent subspace Analysis (ISA) have been applied to model generated and observed time-series. For instance, we have shown that such techniques accomplish an improved separation of dynamical regimes (e.g. weather regimes), as shown in Pires and Ribeiro (2016) (Fig. 3).
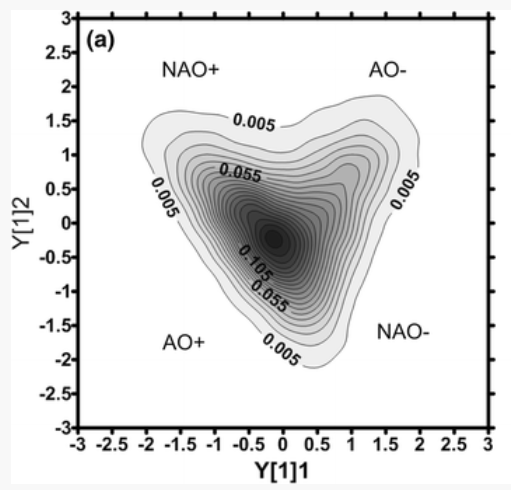
Fig. 3. Pdf contours of a bidimensional statistical source maximizing a quadratic nonlinear correlation. Data consists in geopotential coming from a quasi-geostrophic model. Quadrants correspond to typical North-hemispheric regimes (Pires and Ribeiro, 2016).
The Independent Component & Subspace Analysis (ICA & ISA) have also been applied to monthly SST data covering the global Ocean (Pires and Hannachi, 2017). That is accompanied by highly robust statistical tests to maximally reduce any artificial effects of the sample finiteness and of the Curse of Dimensionality. Then, statistically independent patterns, maximizing nonGaussianity are coming out, revealing nonlinear correlations and joint extremes between patterns which could not be obtained by a single EOF analysis (e.g. nonlinear relationships between the El NiŮo and other Pacific-basin oscillating modes (Fig. 4)).
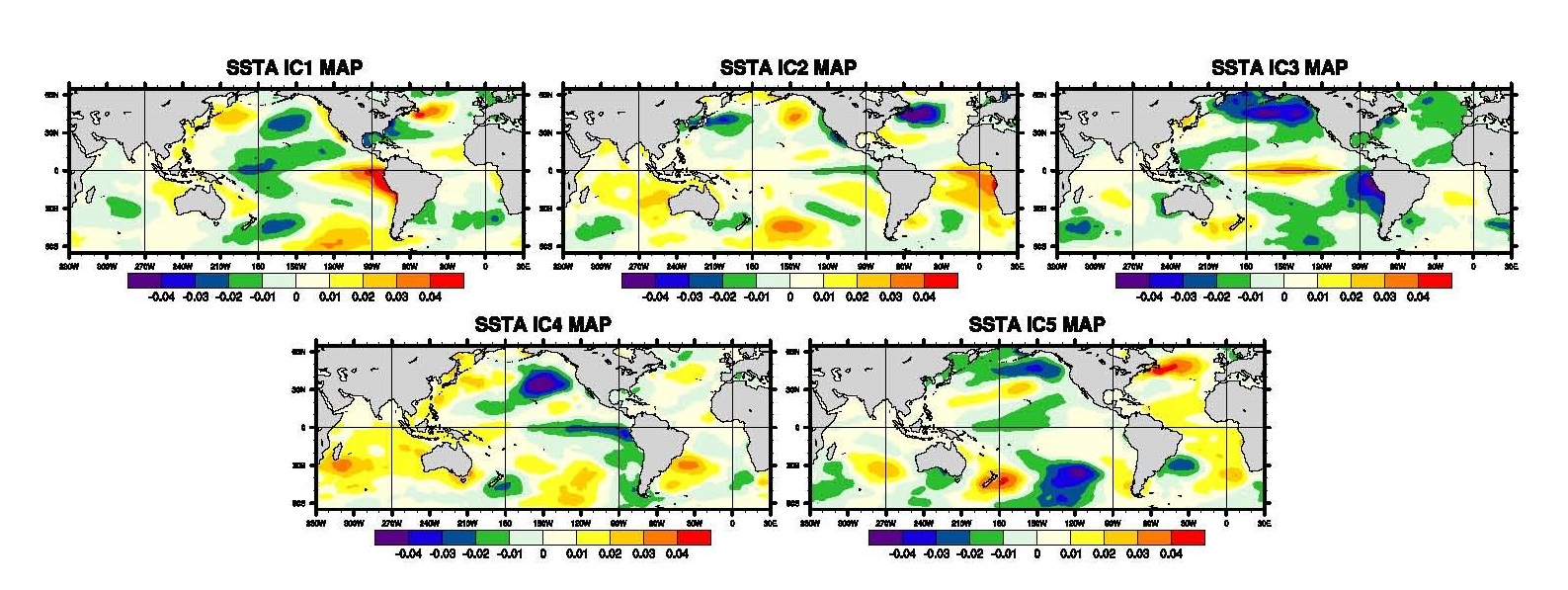
Fig. 4. Weights of the leading 5 statistically independent modes of the monthly SST variability throughout the global Ocean (Pires and Hannachi, 2017).
Many atmospheric-oceanic data assimilation techniques have been optimized under the assumption of Gaussian probability distributions. However, certain assimilated variables and their errors appear to be fit by non-Gaussian pdfs. This idea led us to assess the potential improvement and analysis error reduction due to a non-Gaussian ECMWF data assimilation scheme applied to the assimilation of brightness temperatures coming from the High Resolution Infrared Sounder (HIRS) (Pires et al. 2010). Other relevant data assimilation non-Gaussian techniques have been tested in Bocquet et al. (2010).
References and related works